Polar Coordinates

Definition

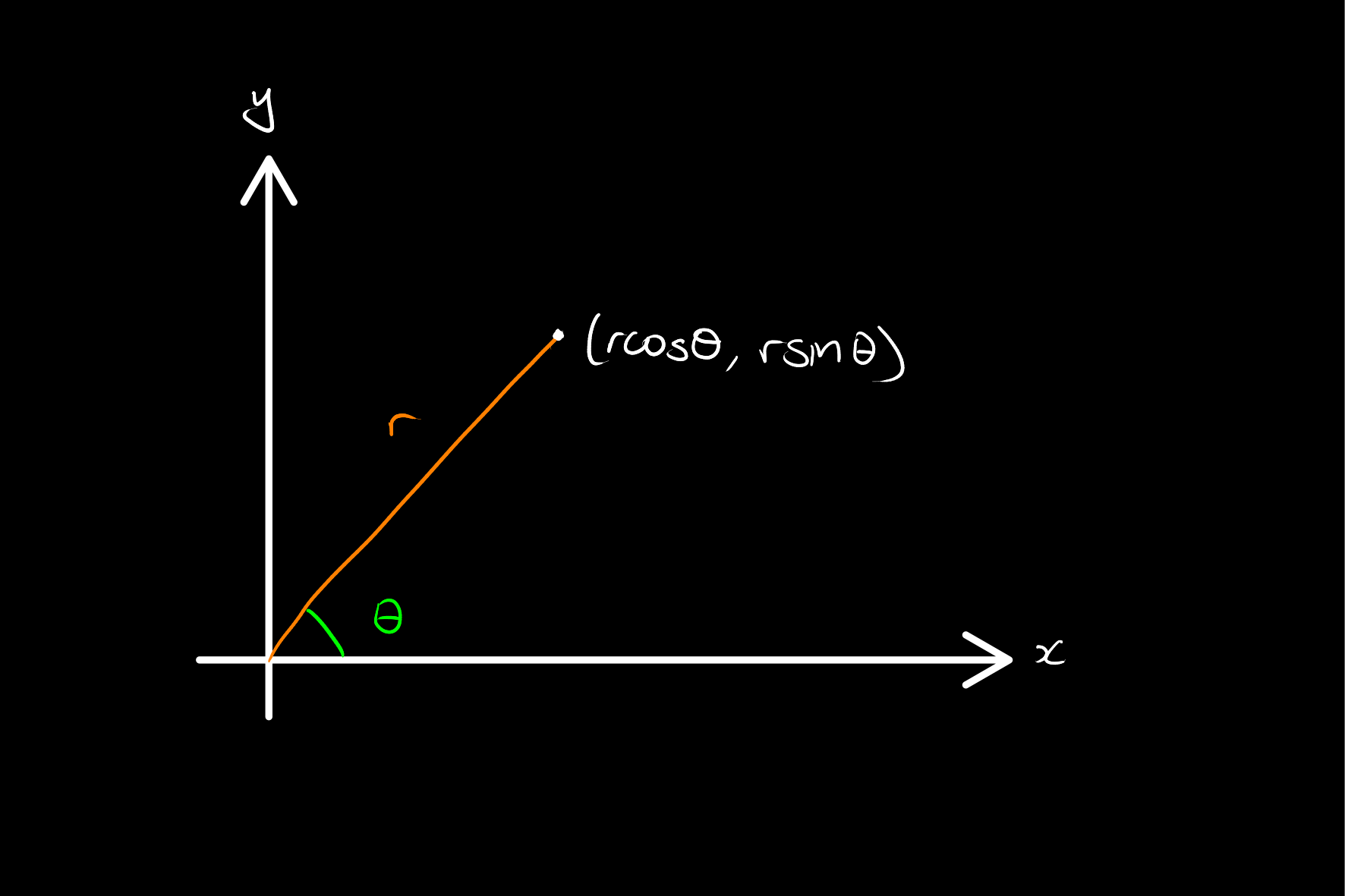
Polar coordinates are a coordinate system for R2 in which a point is defined by its distance from the origin and the angle to a reference direction. In particular, we represent coordinates as the image under the map

F(r,θ)=(rcos⁡(θ),rsin⁡(θ)).
Theorem

Given coordinates of the form (x,y)=(rcos⁡(θ),rsin⁡(θ)), r is uniquely defined up to sign, and if r≠0, then θ is uniquely defined up to an integer multiple of 2π.

Proof

Suppose that x=rcos⁡(θ) and y=rsin⁡(θ). It is clear that

(xr)2+(yr)2=x2+y2r2=1⟹r2=x2+y2⟹r∈{±x2+y2}.

Now, suppose that there are two angles θ and φ such that x=rcos⁡(θ)=rcos⁡(φ) and y=rsin⁡(θ)=rsin⁡(φ). Then, we have that

cos⁡(θ−φ)=cos⁡(θ)cos⁡(φ)+sin⁡(θ)sin⁡(φ)=x2r2+y2r2=x2+y2r2=1.

Hence θ−φ=2πn.

From the above, it is typical to restrict to r≥0 and θ∈[0,2π), and enforce if r=0 then θ=0, as to construct uniquely defined coordinates.